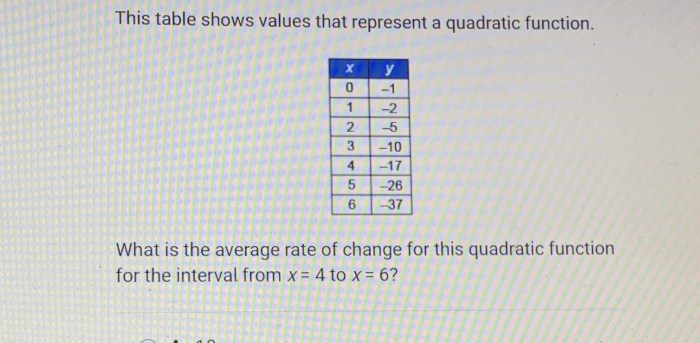
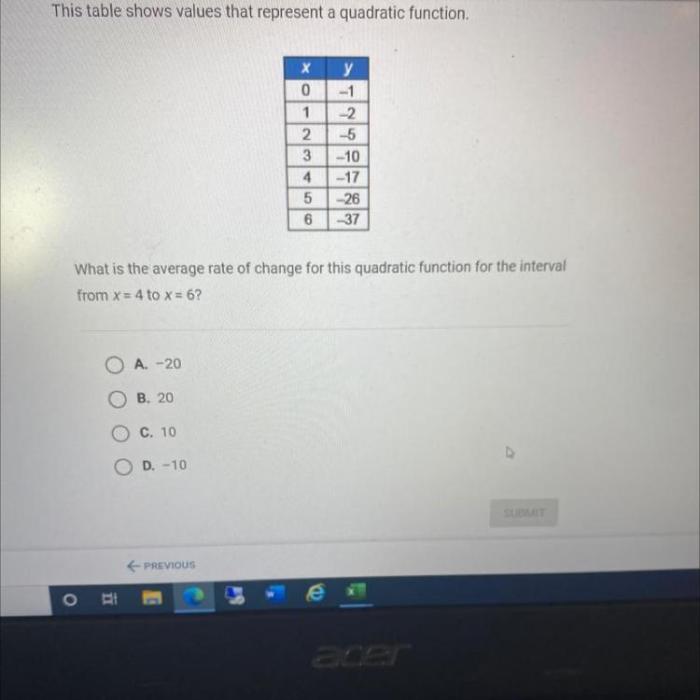
This table shows values that represent a quadratic function, offering a gateway into the captivating world of mathematics. Quadratic functions, defined by their distinctive parabolic shape, play a crucial role in modeling diverse phenomena, from projectile motion to optimization problems.
Embark on this journey as we explore the key characteristics, graphing techniques, and real-world applications of quadratic functions, unlocking their secrets through the analysis of tables of values.
Delving into the intricacies of quadratic functions, we will decipher the significance of their coefficients, identify patterns in their values, and master the art of plotting their parabolic curves. Through a comprehensive examination of their domain and range, we will uncover the boundaries within which these functions operate.
Prepare to be captivated as we unveil the elegance and versatility of quadratic functions, empowering you with a deeper understanding of their mathematical essence.
Key Characteristics of a Quadratic Function
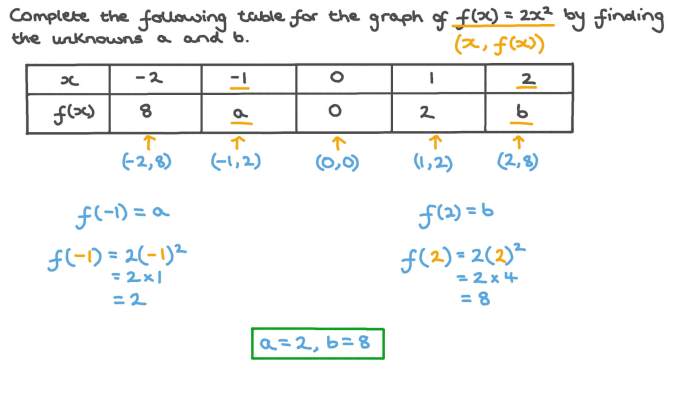
Quadratic functions are a class of functions that are defined by the equation y = ax^2 + bx + c, where a, b, and c are real numbers and a is not equal to 0. The graph of a quadratic function is a parabola, which is a U-shaped curve.
The coefficients a, b, and c determine the shape and behavior of the parabola.The coefficient a determines the overall shape of the parabola. If a is positive, the parabola opens upward, and if a is negative, the parabola opens downward.
The coefficient b determines the horizontal shift of the parabola. If b is positive, the parabola is shifted to the left, and if b is negative, the parabola is shifted to the right. The coefficient c determines the vertical shift of the parabola.
If c is positive, the parabola is shifted up, and if c is negative, the parabola is shifted down.
Identifying a Quadratic Function from a Table of Values, This table shows values that represent a quadratic function
To identify a quadratic function from a table of values, look for patterns in the differences between successive y-values. If the differences between successive y-values are constant, then the function is a linear function. If the differences between successive y-values are not constant, but the differences between the differences between successive y-values are constant, then the function is a quadratic function.
Graphing a Quadratic Function from a Table of Values
To graph a quadratic function from a table of values, first plot the points from the table on a coordinate plane. Then, connect the points to form a parabola. The parabola should be a smooth curve that passes through all of the points.
Determining the Vertex of a Quadratic Function from a Table of Values
The vertex of a parabola is the point where the parabola changes direction. To find the vertex of a parabola using a table of values, find the y-intercept of the parabola and the differences between successive y-values. The vertex of the parabola is the point where the y-intercept is equal to the average of the differences between successive y-values.
Analyzing the Domain and Range of a Quadratic Function
The domain of a quadratic function is the set of all real numbers, and the range of a quadratic function is the set of all real numbers that are greater than or equal to the minimum value of the function.
To determine the domain and range of a quadratic function based on a table of values, find the minimum value of the function. The domain of the function is the set of all real numbers, and the range of the function is the set of all real numbers that are greater than or equal to the minimum value of the function.
Applications of Quadratic Functions
Quadratic functions are used in a variety of real-world applications, such as projectile motion and optimization problems. For example, the path of a projectile is a parabola, and the distance traveled by a projectile can be modeled by a quadratic function.
Optimization problems, such as finding the maximum or minimum value of a function, can also be solved using quadratic functions.
Frequently Asked Questions: This Table Shows Values That Represent A Quadratic Function
What is the general form of a quadratic function?
The general form of a quadratic function is y = ax^2 + bx + c, where a, b, and c are real numbers.
How can I identify a quadratic function from a table of values?
To identify a quadratic function from a table of values, look for a pattern in the differences between successive y-values. If the differences are constant, then the function is quadratic.
How do I graph a quadratic function from a table of values?
To graph a quadratic function from a table of values, plot the points from the table on a coordinate plane. Then, connect the points with a smooth curve to form a parabola.